Circular 674
Thomas Jenkins and Gabriel Bolivar-Mendoza
College of Agricultural, Consumer and Environmental Sciences and College of Engineering, New Mexico State University
Authors: Respectively, Professor and Graduate Student, Department of Engineering Technology and Surveying Engineering, New Mexico State University. (Print friendly PDF)
Overview
This user manual and accompanying Microsoft Excel spreadsheet https://pubs.nmsu.edu/_circulars/CR674/CR674.xlsm are intended to be used as a guide for calculating solar time, angles, and irradiation, and to aid in feasibility and implementation decisions for solar energy projects. The spreadsheet is designed to allow you to enter a variety of values such as system location (i.e., latitude and longitude angles), date, local time, panel tilt angle, etc. By entering different values, you can investigate a variety of scenarios before making final implementation decisions.
There are NO expressed or implied guarantees with this spreadsheet/user manual, nor is it intended to replace professional expertise. It is important to note that the system is designed using some average values. Specific values may vary, and this spreadsheet should ONLY be used as an educational tool.
The spreadsheet consists of different “sheets” or pages that are indexed via tabs at the very bottom of the spreadsheet window. There is a title sheet and five sheets that represent the five main sequential steps in the calculation methodology (Figure 1). The currently selected sheet has a white background, and in Figure 1 this is the Title Page sheet.

Figure 1. Different sheet tabs within the spreadsheet.
On each sheet, there are different shaded boxes, areas, or spreadsheet cells. There are light-purple shaded areas that are instructions and user notes that you should read when using each sheet. The green cells are where you can enter information. To enter a value, move the cursor and click on the green cell (or box), enter your value in that cell (typically a number), and press the “enter” or “return” key on your keyboard.
Some cells have a red triangle in their top right corner. When you place the cursor onto that cell, a “pop-up” note is displayed giving an additional short explanation related to that cell. Some cell entries are restricted in their allowable values. For example, the “Hr” cell in the Time sheet (Figure 3) will only accept entries between 0 and 23. If you enter a value outside this range, an error message will be displayed and you must re-enter a valid value in this cell before continuing.
Some cells may also have a “drop-down” menu associated with them. A drop-down menu will list the cell’s valid entries and allow you to just click on a menu entry. A cell’s menu can be accessed by placing the cursor on the cell and clicking on it. A note and a drop-down menu tab are displayed to the right of the cell. When this tab is clicked, the drop-down menu displays the valid entries for this cell. Just move the cursor and click on any menu entry to make it the cell’s input value.
Finally, orange boxes display intermediate values that are calculated by the spreadsheet, while yellow boxes show the final calculations in this design step.
Step-by-Step Design Procedure
Step 1. Determine the Solar Time and Angles at a Specific Location and Date
Begin by opening the spreadsheet and clicking on the Title Page sheet (the left-most tab at the bottom of the spreadsheet; see Figure 1). Read the title page material and view the solar energy internet videos. Next, continue to the first design sheet by clicking on the Time sheet tab at the bottom of the spreadsheet (Figures 2 and 3).

Figure 2. Time sheet (part 1).
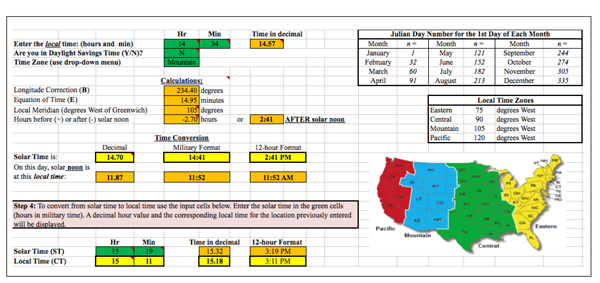
Figure 3. Time sheet (part 2).
The purpose of the Time sheet is to determine the solar time at a given location and time. Solar time depends on the sun’s position and is different from “clock” or “local” time. For example, solar noon is when the sun is at its highest point during the day—when it is at true south in the sky 1. The input cells in the top-right box allow you to specify your exact location by entering the latitude and longitude as well as the date of interest. The spreadsheet will automatically calculate the corresponding Julian day, which is used in subsequent calculations. Julian days are the ordinal number of the day of the year, starting with 1 on January 1st and ending with 365 on December 31st. The spreadsheet is designed to only accept values for latitudes and longitudes within the continental U.S.
The time entry cells allow you to input the local time, time zone, and whether Daylight Saving Time is active on the specified date. The time must be entered in 24-hour format. A map and a table located at the bottom-right of the sheet can be used as an aid to enter the time zone. Using the entered values, the spreadsheet will calculate solar time, angles, and irradiation (i.e., sunlight intensity) in the corresponding sheets. The spreadsheet shows some intermediate calculations and displays the solar time highlighted in yellow. It also displays the local time at which solar noon occurs. Finally, at the bottom of the sheet there are two more input cells that allow you to convert from solar to local time. This time must be entered in 24-hour format as well, and the local timevalue will be shown highlighted in yellow at the bottom of the sheet.
Move to the next sheet titled Angles (Figure 4), which automatically calculates the solar angles relative to the position of the sun in the sky at the specified time and location. The spreadsheet calculates the sun angles at two different times of day. The first is at solar noon, when the sun reaches its maximum altitude in the sky and irradiates the maximum energy for that day. The second is at the given local time. You DO NOT have to enter any values within this sheet.
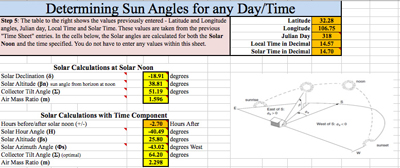
Figure 4. Angles sheet.
Sun angles depend upon the day, time of day (solar time), and latitude location. Solar declination (δ) is the angle formed between the plane of the equator line drawn from the center of the sun to the center of the earth. This angle varies between ±23.45° on the summer (June 21) and winter solstices (December 21), and is 0° on the two equinoxes (March 21 and September 21). The altitude angle (β) is determined by measuring the angle between the sun and the local horizon directly beneath the sun. The solar azimuth angle (Φs) is the angle formed between the current east/west position of the sun from true south, where true south is used as the reference in the northern hemisphere and has a 0° relative angle. A positive azimuth angle is before solar noon and a negative angle is after solar noon; remember that solar noon is when the sun is pointing true south. The hour angle (H) is the number of degrees the earth must rotate before the sun is directly over the local latitude. The air mass ratio (m) is how much atmosphere the solar radiation has to pass through to reach the earth’s surface. If the sun is directly overhead, the air mass number is 1, indicating one full atmosphere that the sunlight must pass through. If the sun is low in the sky, the air mass number will be greater than 1 since the angle causes the sun to pass through more atmosphere, resulting in a loss of solar insolation. Finally, the optimal tilt angle (Σ) is the angle at which the solar panel needs to be set to collect the most energy from the sun. Figure 5 illustrates these angles.
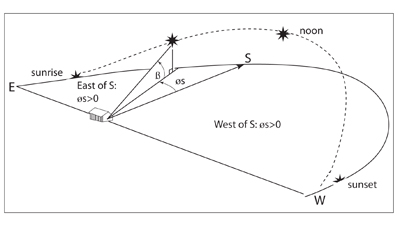
Figure 5. Altitude and azimuth solar angles. Source: Masters, 2004.
Step 2. Determine Total Insolation on a Panel
Navigate to the next sheet titled Insolation (Figure 6), whose purpose is to calculate the amount of solar energy available depending on the date, time, location, and angle configurations of the previous sheets.
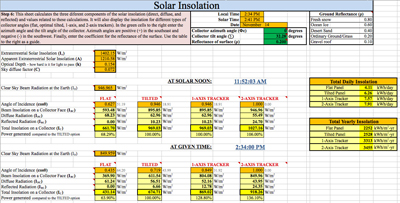
Figure 6. Insolation sheet.
In the green cells at the top of the sheet, input the panel azimuth and tilt angles and the reflectance of the ground surface. Similar to solar azimuth, the azimuth angle of the panel is its +/- angle relative to true south (0°). Tilt angle is the angle the panel is tilted from flat. Finally, the reflectance of the ground surrounding the solar panels must be taken into account because sunlight can reflect off of a surface onto a tilted panel and alter the total solar irradiance collected. The local and solar times, as well as the date entered in the previous sheet, are shown in the box above the green cells as a reference.
Solar irradiation reaches the earth in three different ways: direct, diffuse, and reflected radiation. Each component is affected by several factors, such as the angle of incidence for the direct insolation, sky conditions (e.g., clouds, etc.) for the diffuse radiation, and reflectance of the surface for the reflected radiation. The spreadsheet calculates the amount of radiation for each component depending on the angle or tracker system used to mount the solar panels, then it adds the radiation values and shows the total available insolation reaching that surface and its efficiency compared to the tilted option. The “FLAT” option assumes a solar panel placed parallel to the ground (i.e., horizontal) and it is not affected by any of the previous entries. The “TILTED” option takes into consideration the azimuth and tilt angles. A rule of thumb is to use a tilt angle equal to the latitude of the location; for example, at 32° latitude, the panel would be tilted 32°. The “1-AXIS TRACKER” option assumes that the panels are tilted to an optimal angle (i.e., equal to the latitude) and that they track the sun as it moves across the sky from east to west. Since it tracks the sun, it is not affected by the azimuth angle entry. The “2-AXIS TRACKER” option is not affected by either the azimuth or tilt angles because this system always points the panels directly to the sun in both azimuth and elevation.
At the right of this sheet, two tables are shown. The first table shows the “Total Daily Insolation” for the specified day and location. The spreadsheet sums the insolation for each hour of the day and then adds all these values to get this final value. It is assumed that the insolation remains constant during the entire hour. The “Total Daily Insolation” is shown for the four panel-mounting options (i.e., flat, tilted, 1-axis tracking, and 2-axis tracking). The second table shows the “Total Yearly Insolation” for the location. To aid in this calculation, the total insolation for the 15th day of each month is first calculated, and then it is assumed that this mid-month insolation remains constant during the entire month. Finally, the total insolation for each month is calculated and added to get the “Total Yearly Insolation” value, which is shown for each of the four mounting options.
At the very bottom of the sheet, you can enter the physical size and the rated voltage, current, and power values of a solar panel in order to calculate the panel’s efficiency. The spreadsheet takes into consideration the information entered and the total insolation available to predict voltage, current, power, and efficiency values for that solar panel. These predicted values are obtained using standard test conditions (1000 W/m2 irradiance, 25°C cell temperature, and 1.5 air mass ratio; see Figure 7).
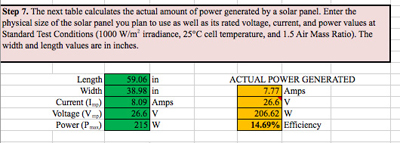
Figure 7. “Actual Power Generated” calculations.
Step 3. Determine the Sun’s Path and the Sunrise and Sunset Hours
Now that the location and calculated angles of the sun at a given time of day have been determined, the position of the sun at any time of day as well as its intensity can be predicted. Using the same method used to calculate the total daily insolation and the position and irradiance of the sun for any time of day, the sunrise and sunset times can also be calculated.
The next sheet, Sunrise-Sunset (Figure 8), determines the sunrise and sunset hours for the given location. This sheet calculates the time the sun begins to be visible before solar noon and the time the sun is no longer visible after solar noon, assuming a flat horizon. Then, this value is used to calculate the solar and local times for the sunrise and sunset. There are two values—geometric and conventional—calculated for both the sunrise and sunset times. The geometric values are obtained using angles measured to the center of the sun, which means that the calculations represent the time when the center of the sun crosses the horizon. The conventional sunrise and sunset values are influenced by an adjustment factor, which takes into consideration atmospheric refraction as well as other atmospheric conditions that make the sun appear to rise sooner and set later. The total time the sun is visible is shown at the bottom of the sheet.
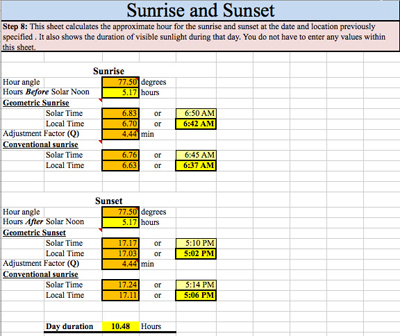
Figure 8. Sunrise-Sunset sheet.
Next, navigate to the Position sheet, where graphs showing the position of the sun at any time of the specified day are displayed (Figure 9). These graphs are obtained by plotting the hourly values of insolation, angles of the sun, and time of day. There are separate graphs for insolation, time, azimuth angle, and altitude angles to ease the reading these values. With these graphs you can analyze and determine sun values at any time of the day at the given location.
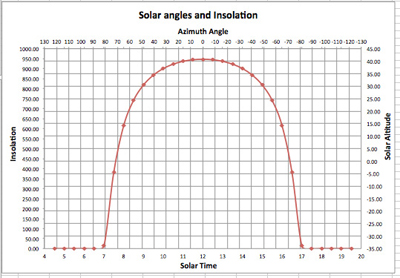
Figure 9. Example of a graph in the Position sheet.
We’re Done
Now you have gone through the process of determining solar angles, insolation, and time values, as well as the position of the sun at any time of day. If you want, print out the calculated values before closing the spreadsheet. Remember that this is an educational tool and should only be used in that manner. If you need further assistance, you can contact local solar installers, the NMSU College of Engineering’s Engineering NM program, or your local county Extension agent.
References
Masters, G.M. 2004. Renewable and efficient electric power systems. Hoboken, NJ: John Wiley & Sons, Inc.
National Renewable Energy Labs. 1997. Electricity when and where you need it: From the sun: Photovoltaics for farms and ranches [Online; NREL/BR-412-21732]. Available from https://www.nrel.gov/docs/gen/fy97/21732.pdf
Internet Links
NMSU YouTube Videos on Renewable Energy Topics: http://www.youtube.com/playlist?list=PL89870B418A514D27
Acknowledgments
The authors wish to express extreme gratitude for the assistance of the NMSU College of Engineering and Engineering NM, NMSU Cooperative Extension Service (https://extension.nmsu.edu), New Mexico Space Grant Consortium (https://www.nmspacegrant.com), Southwest Technology Development Institute (https://ece.nmsu.edu/research/swtdi/), and NMSU Department of Engineering Technology and Surveying Engineering (https://et.nmsu.edu).
1This is for the northern hemisphere. True south is different than magnetic south. (Back to top)

Thomas Jenkins has been a professor in NMSU's Department of Engineering Technology and Survey Engineering since 1990. He previously worked for many years in both private and public sectors as a computer scientist and engineer. Professor Jenkins lead the effort to develop the College of Engineering Renewable Energy Technology minor and helped establish the NMSU student organization Engineers Without Borders.
Disclaimer: This document is intended for educational purposes only, i.e., to provide a basic understanding of terminology and concepts of design. It is not intended to be used beyond this purpose. The author tried to use good engineering analysis; however, all situations are different, and you should consult a professional in all cases.
To find more resources for your business, home, or family, visit the College of Agricultural, Consumer and Environmental Sciences on the World Wide Web at pubs.nmsu.edu.
Contents of publications may be freely reproduced for educational purposes. All other rights reserved. For permission to use publications for other purposes, contact pubs@nmsu.edu or the authors listed on the publication.
New Mexico State University is an equal opportunity/affirmative action employer and educator. NMSU and the U.S. Department of Agriculture cooperating.
September 2014 Las Cruces, NM